2022数模B题——方形件组批优化问题
该题下料优化问题(也称排样优化问题):根据同一生产批次内方形件的尺寸与数量,选择原片的规格和数量,进行下料排样优化,最大化板材原片利用率。依据切割工序的工艺要求,排样方案必须满足“一刀切”(也称齐头切,Guillotine cut)约束(任何一次直线切割都要保证板材可分离,换言之,每次直线切割使得板材分成两块)。下料优化问题属于具有“一刀切”约束的板型材方形件排样优化问题。
常用的解决方案包括启发式迭代算法,树形迭代搜索等等,类似问题论文有很多,本文中主要参考了一篇基于优先级的贪婪迭代搜索算法的文章进行实现的。
- 题目1-2 代码合集 代码下载
- 题目1-2代码的视频讲解(46分钟,包含思路、注意事项、代码解释等,内无代码) 视频获取
- 题目1-2代码的文档(12页,包含模型,公式,算法,参考文献,内无代码,缩略图如下所示)文档获取
- B题大集合 资料下载(包含上面所有内容,打包8折优惠)
(点击上述超链接后,完成后获取卡密即可得到对应地址,以上代码均为matlab平台代码)
咨询请加Q:2479108882(或2438418609)
运行演示
文档缩略图

第一题问题思路与结果:
子问题1:排样优化问题。要求建立混合整数规划模型,在满足生产订单需求和相关约束条件下,尽可能减少板材用量。
约束:
- 在相同栈(stack)里的产品项(item)的宽度(或长度)应该相同;
- 最终切割生成的产品项是完整的,非拼接而成。
- 只考虑齐头切的切割方式(直线切割、切割方向垂直于板材一条边,并保证每次直线切割板材可分离成两块);
- 切割阶段数不超过3,同一个阶段切割方向相同;
- 排样方式为精确排样;
- 假定板材原片仅有一种规格且数量充足;
- 排样方案不用考虑锯缝宽度(即切割的缝隙宽度)影响。



第二题问题思路与结果:
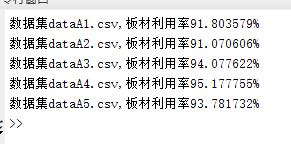
子问题2:订单组批问题。要求建立混合整数规划模型,对数据集B中全部的订单进行组批,然后对每个批次进行独立排样,在满足订单需求和相关约束条件下,使得板材原片的用量尽可能少。在满 面积总和不能超过限定值;
思路:可以考虑将组批问题转换为背包问题和迭代划分问题,采用智能算法进行优化,得到结果如下所示。