本案例中使用Matlab软件对FastICA算法的声音分离性能进行了仿真,分别对简单波形的混合信号、不同类型声音的混合信号、同一类型的混合信号这三种情况进行仿真,主要从分离信号的波形形状、串音误差两方面对分离性能进行衡量,仿真结果显示快速ICA算法分离效果还不错,且算法收敛速度较好。
1 简单波形分离仿真
首先是对简单波形的混合信号进行分离,这里混合信号采用的是方波、三角波和正弦波,这三种波形的频率分别为300hz、400hz、500hz,信号的采样频率为44.1khz,输入原信号序列长度为1000,混合矩阵利用Matlab随机生成,以下是输入的原信号,混合后的信号和分离后信号的波形图。
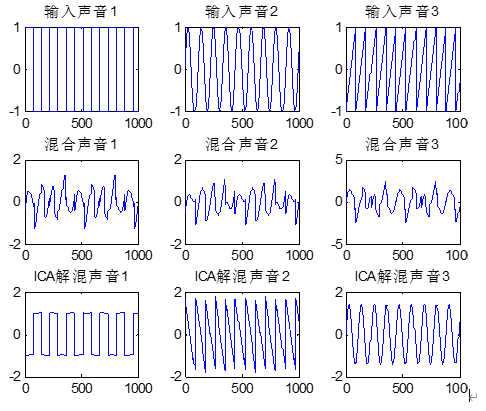
图 5 简单波形的混合信号的分离仿真图
从波形上可以看出,除了幅度和正负由一定的变化外,快速ICA算法对简单波形的混合信号的分离效果还是可以接受的。
2 对不同类型的声音的分离仿真
这里我们对了人声、音乐声和电影特效声音这三种不同类型的声音的混合信号进行分离,输入信号长度为10秒,采用频率为44.1k。其线性瞬时混合模型信道的随机混合矩阵A为

以下是原信号,混合后信号和分离信号的波形图
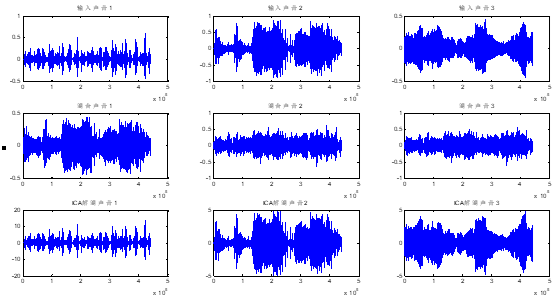
图 6不同类型的声音的分离仿真信号波形图
利用快速ICA算法对这三种不同类型的声音进行分离时,计算所有分量的分离向量的迭代次数为39次,相应的算法分离的串音误差为-23dB。
3 同类型声音的仿真
这里选取的从同一部影视作品中截取的两段不同人物的语音(无背景音乐部分)进行混合和分离,输出信号长度为4.5秒,采样频率同样为44.1Khz。其原信号、混合信号和分离后信号的波形如图
此时,快速ICA算法计算所得的计算所有分量的分离向量的迭代次数为12次,相应的算法分离的串音误差为-47dB。
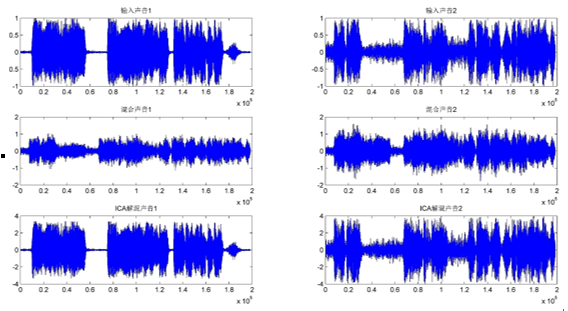
图 7同类型的声音的分离仿真信号波形图